萌新眼中的计算机与机器学习（一）图文重制版

昨晚文章发布之后大家在评论区提出了很多意见，其中最主要的大概就是缺少配图，以及没有机器学习相关的内容。所以我又重做了这一期图文重制版，希望大家能继续给我建议，每条评论我都有看。

另外前两期应该确实不会涉及机器学习相关的干货……因为其实我是想从图灵开始讲述“计算机”是如何从一个只会加减乘除的机器到现在拥有ChatGPT这样的”智能“的。然后就是再次强调我只是一枚大二本科生，知识面和相关见解都非常有限而且粗浅，所以写出来的东西价值不及大佬十一，大家可以把它们当作睡前读物或者交流贴，有错误甚至谬论也很正常，希望大家能在评论区或者私信给我指正，谢谢大家！

图灵与可计算理论

1.写在算法之前

首先是要介绍图灵的”哲学思想“——什么样的问题是可以用算法解决的？

”算法“一词，在数据结构教材中有着详细而恰当的定义，但对于我们理解计算机来说，只需要把握最核心的一点就够了——算法就是按顺序一步一步解决问题的方法。

在过去算法受到重视以前，如牛顿的时代，数理问题的解决主要依赖于天才们一闪而过的灵感与惊人的创造力。对于复杂的问题，他们总能以敏锐的洞察力和高超的技巧发现并揭示问题的核心，并将其转化为易于理解和处理的问题加以解决。比如下图给出的欧拉关于巴塞尔问题的求解方法：

1975年，年仅28岁的欧拉得到了巴塞尔问题的正确解，解决了这个曾困扰牛顿和莱布尼茨等大神的难题

巴塞尔问题是指所有自然数平方的倒数之和的极限是多少的问题。在上面欧拉给出的解法中，最妙的地方之一就在于欧拉对正弦级数和根与系数关系的深刻把握。但问题也显而易见，对大多数人来说，怎么把它们和巴塞尔级数联想到一起呢？

在牛顿到高斯的时代，上述天才”灵光乍现“的例子还数不胜数，这一过程固然富有观赏性，但我们也不难想象缺乏这般天赋的大多数人对此只能望洋兴叹。

2.算法——机器的福音

然而算法的思想却与上述解题过程截然相反——算法是设计好的步骤的集合，任何人（当然，机器也一样）只要老老实实按照顺序执行这些步骤，最终都能得到正确答案。比如下面这个判断一个自然数n是否是素数的算法(这里假定1是素数)：

步骤1.给定n，如果 n = 1，则返回 true，算法结束

步骤2.如果 n = 2 或 n = 3，则返回 true ，算法结束

步骤3.对于每个 i 从 2 到 n-1，依次执行以下步骤： 

                  如果 n 能被 i 整除，则返回 false ，算法结束

步骤4.步骤3中的n-1个数都不能整除n，返回 true，算法结束

在上述算法中，”返回”代表我们找到了问题的答案。返回“true"代表n是素数，返回”false"代表n不是素数，找到问题答案后，紧跟着的就是“算法结束”。

比如对于35，我们依次执行上述算法：

步骤1.给定35，如果35! = 1，继续执行步骤2

步骤2. 35!=2且35!=3，继续执行步骤3

步骤3.对于每个 i 从 2 到 n-1，依次执行以下步骤： 

                  初始时，i=2，35不能被2整除，i=2+1=3；

                  i=3,35不能被3整除，i=3+1=4;

                  i=4,35不能被4整除，i=4+1=5;

                  i=5,35能被5整除，返回false,算法结束

步骤4.步骤3已经得到问题答案，无步骤4

所以最终答案是"false"，35不是素数！我们可以惊喜的发现，上述算法只需要掌握三种基本运算即可进行，也即比较运算，+1运算，整除运算。而且只要你是严格按照以上步骤执行而没有遗漏其中某步，最终一定能得到正确答案。虽然我们一眼就能看出来35能被5整除，所以35肯定不是素数，但这个算法的威力就在于，即使是对4294967297（2^32+1）这样可怕的数字，我们只要按照上述步骤执行，最后总能找到正确答案——而这时候，想要通过眼睛观察出4294967297的两个质因数（641和6,700,417）而得到“4294967297不是素数”的结论，就不那么容易了。

总之，算法思想隐含的就是这样一个“福音”——不管“你”有多白痴，只要你会做加减乘除和比较大小之类等基本运算，你都可以按照给定的步骤一步步拆解并最终得到一个复杂问题的正确答案。这不仅对“你”来说是福音，对机器也同样如此。

3.问题来了，什么是“基本运算”？

上面说到算法实现了让一个只会加减乘除等基本运算的“白痴”也能正确地解决复杂问题。那么现在问题又来了，到底什么是“基本运算”？微积分是基本运算吗？矩阵的奇异值分解是基本运算吗？事实上，我们发现这些复杂的数学计算大部分都可以用一系列加减乘除等更基本地运算来加以实现或近似——这没关系，计算机本来就不可能处理一个真正的无理数，因为存储它需要无穷多个存储单元，我们只能在精度允许的范围内得到“正确答案”。而加减乘除等运算又可以进一步分解为若干步的“与或非”等二进制运算（之所以要继续分解，自然是因为计算机只能处理二进制数）——没错，某种意义上这也是一种“算法”——如何用一串有序的二进制运算来实现整数的加减乘除，比较大小。

对计算机来说，什么是最基本的运算？是刚才提到的“与或非”吗？不是的，其实“与门”“或门”“非门”都可以用最简单的门——“与非门”实现（感兴趣的可以学习《离散数学》中的联结词完备集）。而且除了这些逻辑和算术运算之外，我们还需要计算机做其他操作，比如存储数据，读取数据，等等，这些“基本操作”的定义随着我们的需求的变化不一而足。下图是一个简单的模型机的指令集，它给出我们对计算机所理应能够执行的“基本运算”（说操作/指令也许更合适）的较低期望：

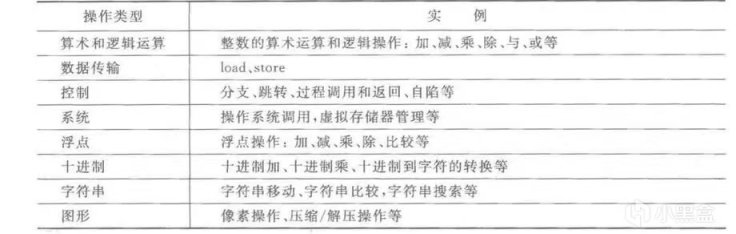
指令系统结构中操作的分类

对于“基本操作”的问题，尤其是我们很关心的指令集完备性问题，以及如何用二进制与或非运算实现整数的加减乘除的问题，在《计算机组成原理》这门课中还会有详细的讨论，在此就不再继续展开了（应该是可以的吧……）

4.小结

至此我们讨论了算法的底层思想和它是如何对计算机起作用的。但我们并不欲回答开篇的问题——“什么样的问题是可以用算法解决的”。这是一个相当困难而复杂的问题，还与千禧年7大难题之一的“NP猜想”有关，至少笔者还没有能力触及该问题的皮毛。不过可以肯定的是，一定有问题是不能用算法解决的，比如著名的“停机问题”。关于这方面的知识，有兴趣的读者可以自行学习《形式语言与自动机》，该问题相应的理论是开头提到过的计算机科学的一大分支“可计算性理论”。

不过以上讨论对我们来说已经够用了，我们知道了什么是算法，而且我们确实发现许许多多的问题都可以用算法解决——对我们来说，剩下的任务就是将算法国度的疆界不断扩大，不断创造/发现算法去解决各种各样的问题。当然在此之前还有一个问题是留待下一篇帖子解决的——我们怎样实现计算机自动地执行算法？（或者说，“计算器”与“计算机”的区别在哪里？）

PS：人类历史上最早的算法大约可以追溯到两河流域的美索不达米亚文明，那时的美索不达米亚人已经发明了求根号2的算法，下面是某中学教材中对此算法的说明，读者可自行探究其原理及正确性。

美索不达米亚人的开根号算法

另外楼主本人水平十分有限，再次感谢大家的阅读，有不妥甚至错误的地方请大家在评论区指出或者私信我，我每条评论都有认真看！谢谢大家的鼓励和建议！！！下一篇我打算将冯诺依曼和数字化——计算机如何像人类一样处理各种（听觉，视觉等的）信息，离讲到正题机器学习恐怕还有点远！但我是想从一切的最开始出发去体会计算机如何从宾夕法尼亚大学的那个笨重的庞然大物蜕变为今天ChatGPT这样的“人工智能”的大家对思路安排上有啥建议可以直接私信我。另外最近期末周恐怕没多少时间写帖子，下一篇不知道要鸽到什么时候了

关于转载：大家最好不要随意转载，因为楼主水平实在太差了，写的帖子很可能漏洞百出，别到了最后以讹传讹就不好了。但欢迎大家针对帖子的内容随意讨论！